Na rysunku przedstawiono fragment wykresu funkcji kwadratowej f

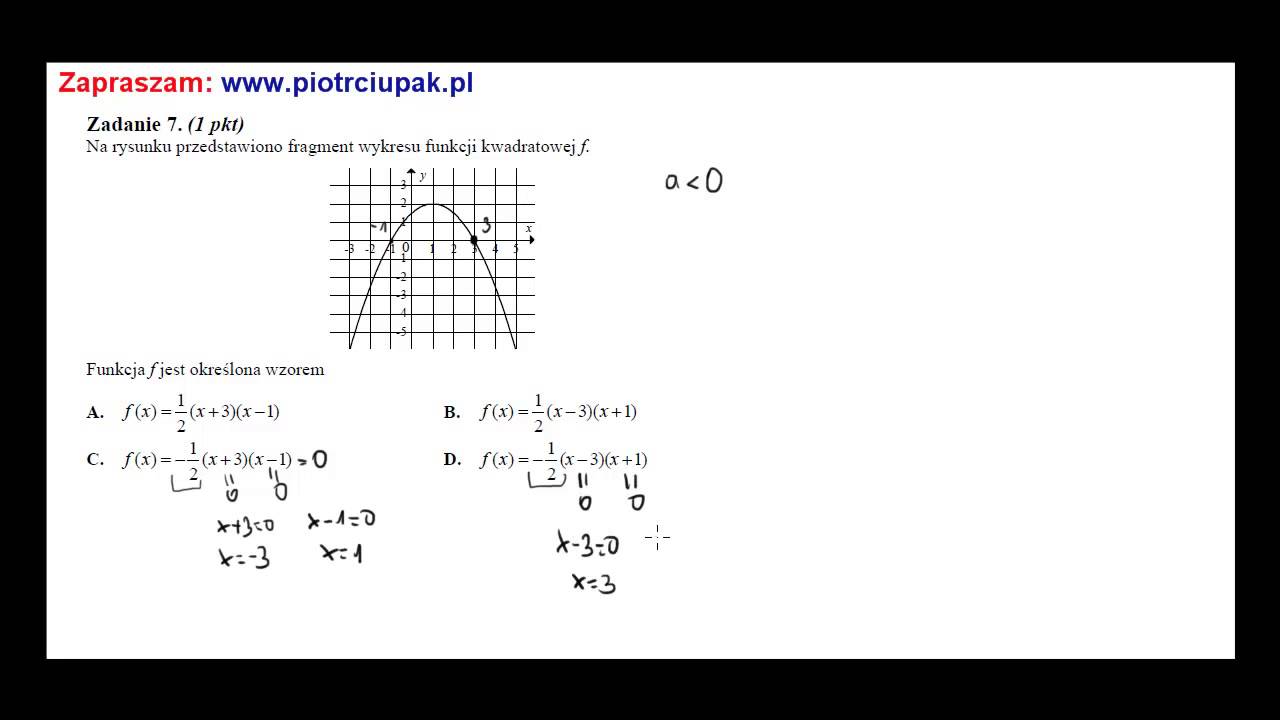
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej f jest tematem często omawianym w szkołach na lekcjach matematyki.

Funkcja kwadratowa jest jedną z podstawowych funkcji matematycznych, a jej wykres jest niezwykle ważnym narzędziem do zrozumienia jej własności.

Funkcja kwadratowa jest funkcją postaci f(x) = ax² + bx + c, gdzie a, b i c są stałymi, a x jest zmienną.

Jest to funkcja wielomianowa drugiego stopnia, co oznacza, że jej wykres jest parabolą.

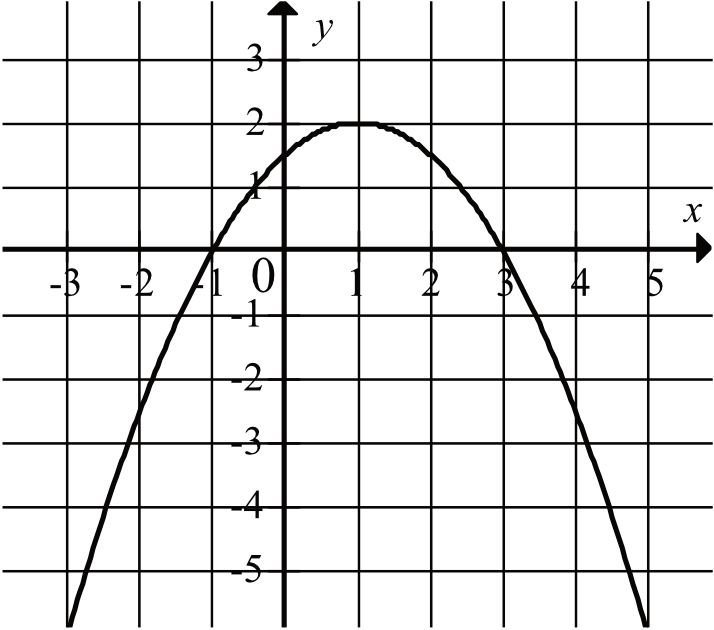
Wykres funkcji kwadratowej jest więc wygiętą linią, która może mieć różne położenie i kształty w zależności od wartości stałych a, b i c.

Na rysunku przedstawiono fragment wykresu funkcji kwadratowej f oznacza, że nie jest to cały wykres, ale tylko jego część. Warto zauważyć, że funkcja kwadratowa może mieć nieskończenie wiele fragmentów wykresu, ponieważ jest to funkcja ciągła.

Dlatego też w praktyce często przedstawiane są tylko jej wybrane fragmenty, aby ułatwić analizę i zrozumienie jej własności.

Na rysunku, oprócz samego wykresu, można również zauważyć inne ważne elementy, takie jak oś x i oś y oraz punkty przecięcia wykresu z nimi.

Oś x jest osią poziomą, a oś y jest osią pionową.

Przecięcie wykresu z osią x oznacza miejsca, w których funkcja przyjmuje wartość 0, a przecięcie z osią y – wartość stałej c.

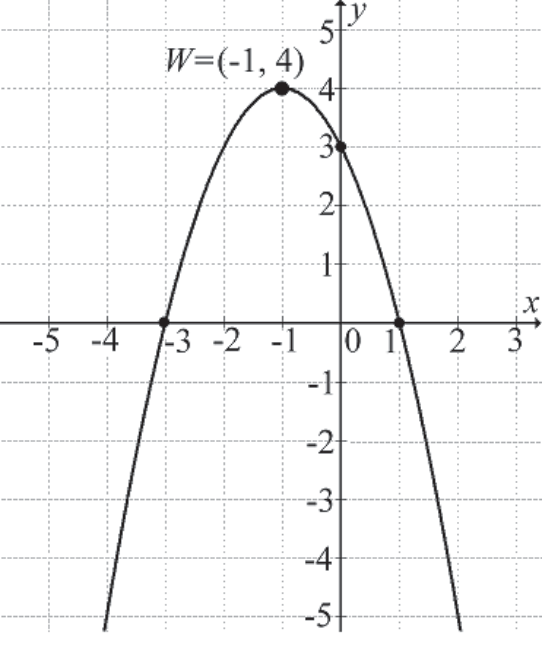
Natomiast punkt przecięcia wykresu z osiami to miejsce, w którym funkcja osiąga ekstremum, czyli wartość największą lub najmniejszą.

Analiza wykresu funkcji kwadratowej jest bardzo ważna, ponieważ pozwala ona na określenie jej własności, takich jak dziedzina, przeciwdziedzina, miejsca zerowe, ekstremum, monotoniczność czy też wypukłość. W.